10 приемов решения квадратного уравнения. Исследовательская работа "10 способов решения квадратных уравнений". Как составлял и решал Диофант квадратные уравнения
Департамент образования и науки
Кемеровской области
ГОУ СПО «Мариинский аграрный техникум»
10 СПОСОБОВ РЕШЕНИЙ
КВАДРАТНЫХ УРАВНЕНИЙ
ах ²+вх+с=0
Работу выполнила:
Король Вера,
обучающаяся группы 161
по специальности 260807 «Технология продукции общественного питания»
Руководитель:
Матвеева Ольга Васильевна,
преподаватель математики
Мариинск, 2013
I. Введение
II. История возникновения квадратных уравнений
2. Квадратные уравнения в Древнем Вавилоне.
3. Квадратные уравнения в Европе XIII – XVII вв.
III. Способы решения квадратных уравнений
3. Частные случаи решения квадратных уравнений:
а) коэффициент а - очень маленький,
б) коэффициент с – очень маленький.
4. Решение уравнений с использованием теоремы Виета.
6. Решение уравнений способом «переброски».
9. Решение квадратных уравнений с помощью номограммы.
IV. Заключение
V. Литература
I. ВВЕДЕНИЕ
«Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».
У. Сойер
Квадратные уравнения – это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении различных тригонометрических, показательных, логарифмических, иррациональных, трансцендентных уравнений и неравенств , большого количества разных типов задач.
Теория уравнений занимает ведущее место в алгебре и математике в целом. Сила теории уравнений в том, что она не только имеет теоретическое значение для познания естественных законов, но и служит практическим целям. Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Квадратное уравнение представляет собой большой и важный класс уравнений, решающих как с помощью формул, так и с помощью элементарных функций.
В школьном курсе математики мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем решение по стандартным формулам. Вместе с тем, современные научно – методические исследования показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений.
Таким образом, возникает необходимость изучения различных способов решения квадратных уравнений.
Все сказанное выше определяет актуальность темы исследовательской работы.
Проблема исследования заключается в рассмотрении различных, в том числе нестандартных способов решения квадратных уравнений.
Цель работы состоит в изучении теоретических основ и их применение при решении квадратных уравнений.
Предмет исследования: квадратные уравнения и их решения.
Задачи:
Провести анализ литературы по данной теме.
Изучить историю развития квадратных уравнений.
Изучить различные способы решений квадратных уравнений в том числе нестандартных и апробировать материал на практике.
II. ИСТОРИЯ ВОЗНИКНОВЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
1. Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются в астрономическом тракторе «Ариабхаттиам», составленном в 499 г. Индийским математиком и астрономом Ариабхатой. Другой индийский ученый – Брахмагупта (VII в.) изложил общее правило решения квадратных уравнений. Правило Брахмагупты по существу совпадает с современным.
В древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в Бхаскары.
Обезьянок резвых стая
Власть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась,
А двенадцать по лианам
Стали прыгать, повисая..
Сколько ж было обезьянок
Ты скажи мне, в этой стае?
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратного уравнений.

х 2 – 64 = - 768,
х 2 – 64х +32 2 = - 768 + 1024,
(х – 32) 2 = 256,
х 1 = 16, х 2 = 48
2. Квадратные уравнения в Древнем Вавилоне.
Квадратные уравнения умели решать вавилоняне около 2000 лет до н.э. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и таких, например, полные уравнения.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденный до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом
они были найдены. Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
3. Квадратные уравнения в Европе в XII – XVII вв.
Формы решения квадратных уравнений по образцу ал - Хорезми в Европе были в первые изложены в «Книге абаха», написанной в 1202 году, итальянским математиком Леонардо Фибоначчи. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из «Книги абаха» переходили почти во все европейские учебники XVI – XVII вв. и частично XVIII в.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х 2 + bx = с при всевозможных комбинациях знаков и коэффициентов b , c , было сформулировано в Европе в 1544 г. М. Штифелем. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни Виет знаменитый француский ученый также по профессии адвокт. Итальянские ученые Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря трудам Жиррара, Декарта, Ньютона и других ученых, способ решения квадратных уравнений принимает современный вид.
III. РАЗЛИЧНЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
1. Общий вид квадратного уравнения и стандартные формулы для его решения.
Уравнение вида ах 2 + вх + с = 0 (1) , где а, в, с - некоторые числа, причем а ≠ 0, называется квадратным.
Квадратное уравнение называют также уравнением второй степени.
В уравнении (1) а называется первым коэффициентом, в – вторым коэффициентом, с – третьим коэффициентом или свободным членом.
Выражение вида D = в 2 – 4ас называется дискриминантом (различителем) квадратного уравнения.
Напомним, что корнем (или решением) уравнения с неизвестным х называется число, при подстановке которого в уравнение вместо х получается верное числовое равенство.
Решить уравнение – значит найти все его корни или показать, что их нет.
Наличие корней квадратного уравнения (1) зависит от знака дискриминанта D , поэтому решение уравнения следует начинать с вычисления D , чтобы выяснить имеет ли квадратное уравнение (1) корни, и если имеет, то сколько.
Возможны три случая:
Если D >0, то квадратное уравнение (1) имеет два различных действительных корня:

 в
2
– 4ас.
в
2
– 4ас.

Если D <0, то квадратное уравнение не имеет действительных корней.
Предположим, что в некотором уравнении мы сделали следующие преобразование: раскрыли скобки, если они есть, уничтожили знаменатели, если в уравнении есть дробные члены, перенесли все члены в левую часть уравнения и сделали приведение подобных членов. Если после этого в левой части уравнения окажется член, содержащий неизвестное в квадрате, и не будет членов, содержащих неизвестное в более высокой степени, то получили квадратное уравнение. Общий вид такого уравнения есть ах 2 + bx + c = 0.
Заметим, что коэффициент а мы всегда можем сделать положительным, переменив в случае надобности перед всеми членами уравнения знаки на противоположные.
Пример 1.
Найдите коэффициенты
а, в
и
с
для уравнения:  .
.
Решение:
Раскрываем скобки: 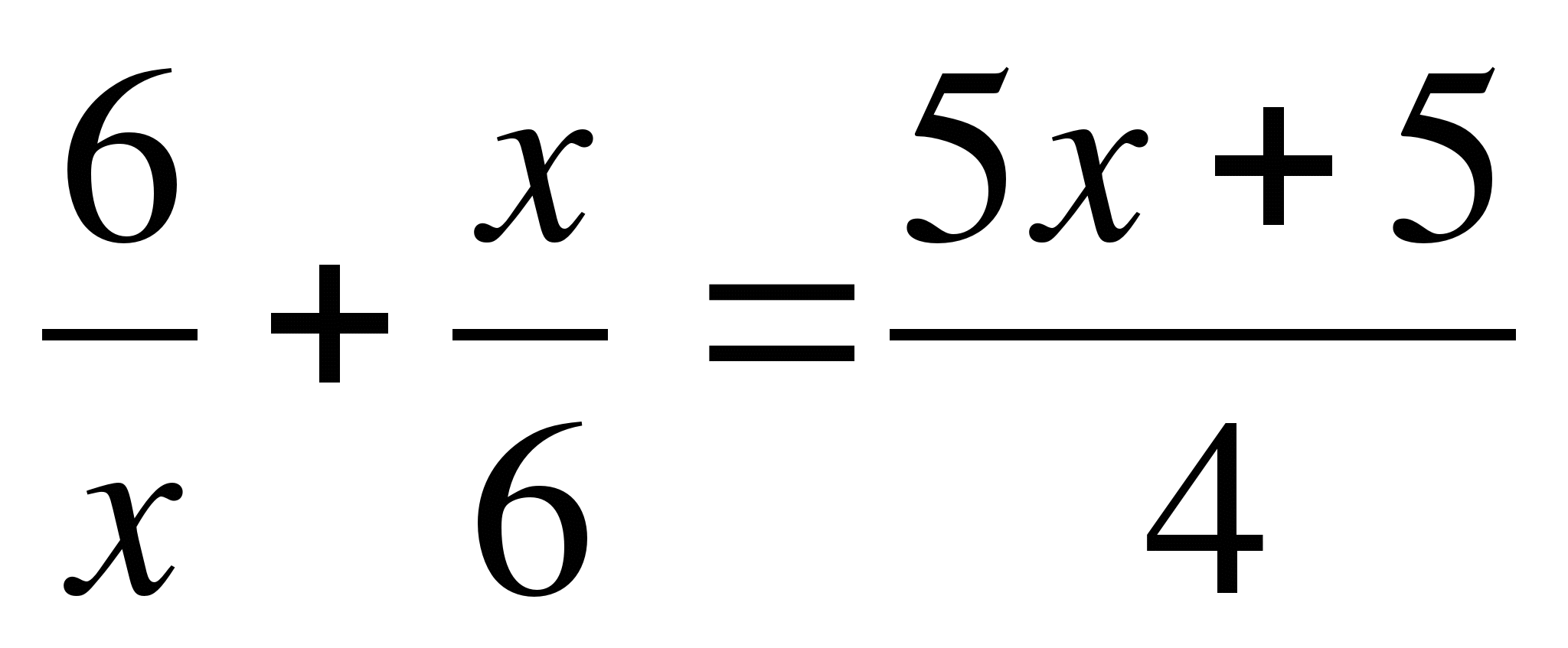 ,
,
Уничтожаем знаменатель: 72 + 2х 2 = 15х 2 + 15х,
Переносим все члены в левую часть и делаем приведение: - 13х 2 – 15х + 72 = 0,
Переменяем знаки: 13х 2 + 15х – 72 = 0,
Коэффициенты а, b , и с общего вида квадратного уравнения приняли в этом примере такие частные значения: а = 13, b = 15 и с = - 72 .
Пример 2.
Решите уравнение: 
Решение: >0, два корня;
Ответ: 
Пример 3.
Решите уравнение: 
Решение: D =0, один корень;

Ответ: 
Пример 4.
Решите уравнение: 
Решение: <0.
Уравнение не имеет действительных корней.
Ответ: нет действительных корней.
Рассматривая решение квадратных уравнений, видим что эти уравнения иногда имеют два корня, иногда один, иногда ни одного. Однако согласились приписывать квадратным уравнениям во всех случаях
два корня
, разумеется при этом, что корни могут быть иногда равными, иногда мнимыми. Причина такого соглашения состоит в том, что формулы, выражающие мнимые корни уравнения, обладают теми же свойствами, какие принадлежат вещественным корням, состоит только совершая действия над мнимыми количествами, руководиться правилами, выведенными для вещественных количеств, принимая при этом, что ( )
2
= - а. Точно так же, когда уравнение имеет один корень, мы можем, рассматривая это корень как
два одинаковых,
приписать им те же свойства, какие принадлежат разным корням уравнения. Простейшие из этих свойств выражают в следующей теореме.
)
2
= - а. Точно так же, когда уравнение имеет один корень, мы можем, рассматривая это корень как
два одинаковых,
приписать им те же свойства, какие принадлежат разным корням уравнения. Простейшие из этих свойств выражают в следующей теореме.
Теорема: Сумма корней квадратного уравнения, у которого коэффициент при неизвестном во 2 – й степени есть 1, равна коэффициенту при неизвестном в первой степени, взятому с обратным знаком; произведение корней этого уравнения равна свободному члену.
Доказательство: Обозначив через α и β корни уравнения х 2 + рх + q = 0 , будем иметь (каковы бы ни были эти корни)


Это произведение можно найти сокращенным путем, основываясь на равенстве (a + b )(a – b ) = a 2 – b 2 :

Если α и β есть корни уравнения ах 2 + bx + c = 0 , или что то же уравнения
 , то будет иметь
, то будет иметь 
 .
.
Обратная теорема: Если количества α, β, р и q таковы, что α + β = - р и αβ = q , то β и α суть корни уравнения х 2 + рх + q = 0 .
Доказательство: Требуется доказать, что каждое из количеств β и α удовлетворяет уравнению х 2 + рх + q = 0 . Из равенства α + β = - р и α = -р – β , после чего равенство αβ = q дает
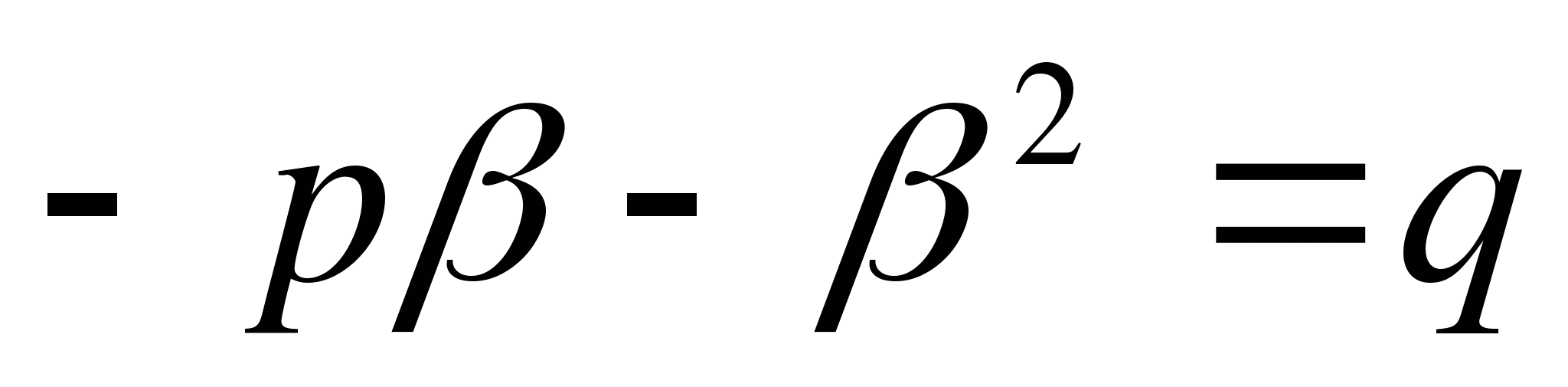 или
или  .
.
Значит, β есть корень уравнения ах 2 + bx + c = 0 ; подобным же образом убедимся, что и α есть корень того же уравнения.
1-е следствие. По данным корням можно составить квадратное уравнение. Пусть требуется составить уравнение, корни которого были бы 2 и – 3. положив, что 2 + (- 3)= - р и 2 · (- 3) = q , находим - р = 1, q = - 6. Значит, искомое уравнение будет
х 2 + х – 6 = 0
Подобно этому найдем, что – 2 и – 2 являются корнями уравнения х 2 + 4х + 4 = 0, 3 и 0 являются корнями уравнения х 2 – 3х = 0 и т. П.
2-е следствие.
Не решая квадратного уравнения, можно определить знаки его корней, если эти корни вещественные.
Пусть, например, имеем уравнение х
2
+ 8х +10 = 0. Так как в этом примере количество  -
q
есть положительное число, то оба корня должны быть вещественные. Определим, не решая уравнения, знаки этих корней. Для этого рассуждаем так: обращая внимание сначала на свободный член (+ 10), видим, что он имеет знак +; значит, произведение корней должно быть
положительное
, т. е. оба корня имеют
одинаковые
знаки. Чтобы определить, какие именно, обратим внимание на коэффициент при
х
(т. е. на +8) он имеет знак +; следовательно, сумма коэффициентов
отрицательна
; потому одинаковые знаки у корней должны быть
минус
.
-
q
есть положительное число, то оба корня должны быть вещественные. Определим, не решая уравнения, знаки этих корней. Для этого рассуждаем так: обращая внимание сначала на свободный член (+ 10), видим, что он имеет знак +; значит, произведение корней должно быть
положительное
, т. е. оба корня имеют
одинаковые
знаки. Чтобы определить, какие именно, обратим внимание на коэффициент при
х
(т. е. на +8) он имеет знак +; следовательно, сумма коэффициентов
отрицательна
; потому одинаковые знаки у корней должны быть
минус
.
Подобными рассуждениями можно определить знаки у корней и во всяком другом случае. Так, уравнение х 2 + 8х - 10 = 0 имеет корни с разными знаками
(потому что их произведение отрицательно), причем отрицательный корень имеет большую абсолютную величину (потому что их сумма отрицательна); уравнение х 2 – 8 – 10 = 0 также имеет корни с разными знаками, но большая абсолютная величина принадлежит положительному корню.
2. Решение неполных квадратных уравнений.
Квадратное уравнение называется неполным, когда в нем нет члена, содержащего х , или нет свободного члена. Неполные квадратные уравнения могут быть только трех следующих видов:
а) ах 2 + с = 0; б) ах 2 + bx = 0; с) ax 2 = 0.
Рассмотрим решение каждого из них.
а) Из уравнения х 2 + с = 0 находит
ах
2
= - с и х
2
=  .
.
Это равенство требует, чтобы квадрат неизвестного равнялся количеству ; значит, неизвестное должно равняться квадратному корню из этого количества. Это возможно только тогда, когда количество
; значит, неизвестное должно равняться квадратному корню из этого количества. Это возможно только тогда, когда количество  есть положительное число, что будет тогда, когда
с
и
а
имеют противоположные знаки (если, например,
с
= - 8,
а
= + 2, то
есть положительное число, что будет тогда, когда
с
и
а
имеют противоположные знаки (если, например,
с
= - 8,
а
= + 2, то 
Условимся обозначать знаком  только арифметическое значение квадратного корня и примем во внимание, что квадратный корень из положительного числа имеет два значения; тогда, обозначая одно значение через
х
1
,
а другое через
х
2
, можем написать
только арифметическое значение квадратного корня и примем во внимание, что квадратный корень из положительного числа имеет два значения; тогда, обозначая одно значение через
х
1
,
а другое через
х
2
, можем написать

Если числа
с
и
а
имеют одинаковые знаки, то количество  представляет собой отрицательное число; тогда уравнение ах
2
+ с = 0 не может быть удовлетворено никаким вещественным числом; в этом случае говорят, что уравнение имеет два
мнимых
корня.
представляет собой отрицательное число; тогда уравнение ах
2
+ с = 0 не может быть удовлетворено никаким вещественным числом; в этом случае говорят, что уравнение имеет два
мнимых
корня.
Пример 5.
Решите уравнение: 3х 2 – 27 = 0.
Решение: 3х
2
= 27; х
2
= 9; х = 
Ответ: х = 
Пример 6.
Решите уравнение: х 2 +25 = 0.
Решение: х
2
= - 25; х =  ; корни мнимые.
; корни мнимые.
Ответ: х = + - 5 i .
б) Чтобы решить уравнение ах 2 + bx = 0 , представим его так х( ax + b ) = 0 . Произведение может равняться нулю только тогда, когда какой – нибудь из сомножителей равен нулю; следовательно, рассматриваемое уравнение удовлетворяется, если положим, что х = 0 или ах + b = 0 /
Второе равенство дает  Итак, уравнение
ах
2
+
bx
= 0
имеет два корня
Итак, уравнение
ах
2
+
bx
= 0
имеет два корня
х
1
= 0 и 
Пример 7.
Решите уравнение: 2х 2 – 7х = 0.
Решение: 2х 2 – 7х = 0, х(2х – 7) = 0; х 1 = 0; х 2 = .
Ответ: х 1 = 0; х 2 = .
в) Наконец, квадратное уравнение ax 2 = 0 имеет, очевидно, только одно решение х = 0.
3.Частные случаи квадратных уравнений.
а) Случай, когда коэффициент а очень мал.
Вычисление корней уравнения ах 2 + bx + c = 0 по общей формуле, выведенной выше, затруднительно в этом случае, когда коэффициент а очень малое число сравнительно с b и с . В самом деле, вычисляя корни по формуле

Мы в большинстве случаев должны довольствоваться приближенной величиной 
 , а следовательно, и всего числителя. Разделив эту приближенную величину на 2а, мы тем самым разделим на 2а и погрешность, с которой вычислен числитель формулы. Но так как, по предложению, 2а очень малая дробь, деление на малую дробь равносильно умножению на большее число, то погрешность значительно возрастает, вследствие чего окончательный результат будет далек от истинного. Если, например, 2а = 0,0001 и мы вычислили
, а следовательно, и всего числителя. Разделив эту приближенную величину на 2а, мы тем самым разделим на 2а и погрешность, с которой вычислен числитель формулы. Но так как, по предложению, 2а очень малая дробь, деление на малую дробь равносильно умножению на большее число, то погрешность значительно возрастает, вследствие чего окончательный результат будет далек от истинного. Если, например, 2а = 0,0001 и мы вычислили  до четвертого десятичного знака, то предел погрешности в окончательном результате будет 0,0001: 0,00001 = 10.
до четвертого десятичного знака, то предел погрешности в окончательном результате будет 0,0001: 0,00001 = 10.
Для вычисления корней уравнения в этом случае употребляется более удобный способ так называемого последовательного приближения.
Заметим, что при очень малой величине
а
один из корней уравнения немного отличается от 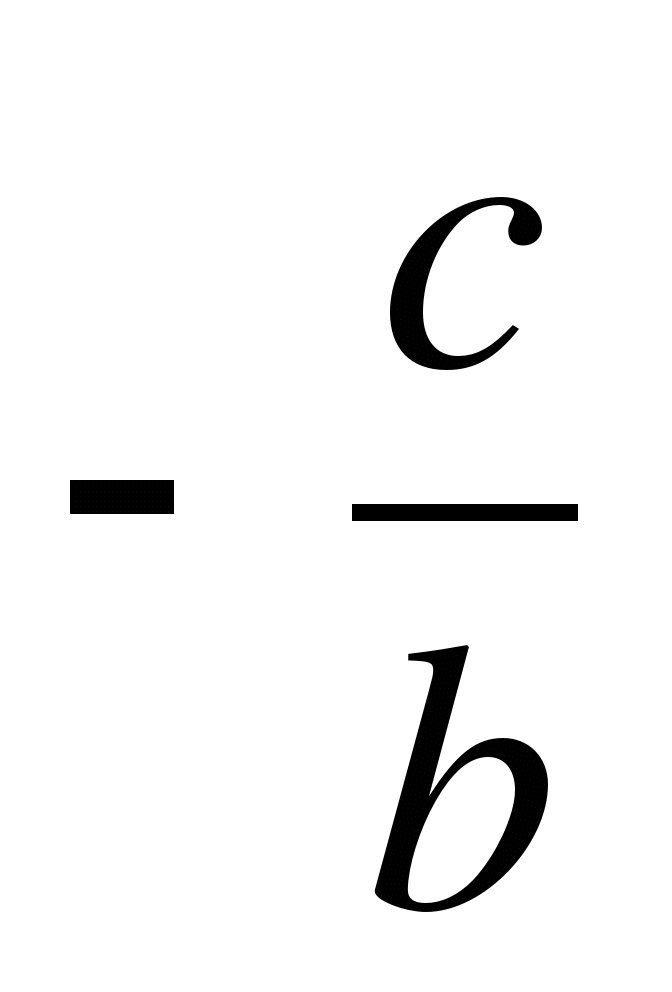 , а другой - весьма большое число (по абсолютной величине). Действительно, уравнение ах
2
+
bx
+
c
= 0 равносильно уравнению
, а другой - весьма большое число (по абсолютной величине). Действительно, уравнение ах
2
+
bx
+
c
= 0 равносильно уравнению
 ,
,
которому можно придать вид

Так как –
а
близко к нулю, то последние уравнение может быть удовлетворено такими значениями
х
, при которых один из сомножителей левой части уравнения окажется очень малым числом, а другой – не очень большим; это будет иметь место или тогда, когда придадим
х
весьма большое абсолютное значение, или же тогда, когда
х
будет близко к 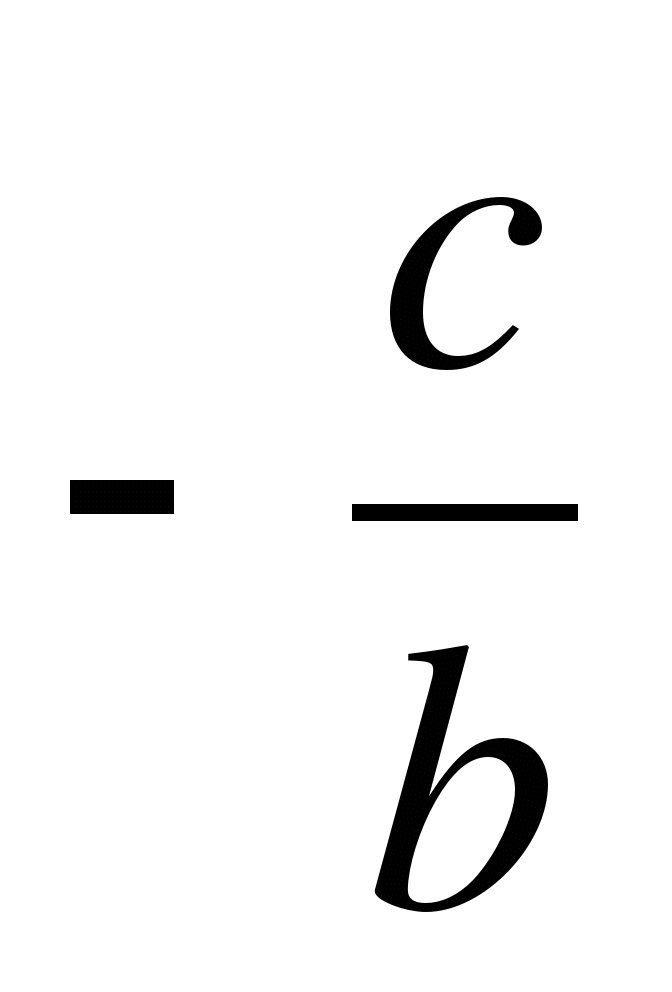 .
.
Покажем, как вычислить тот из корней, который мало отличается от 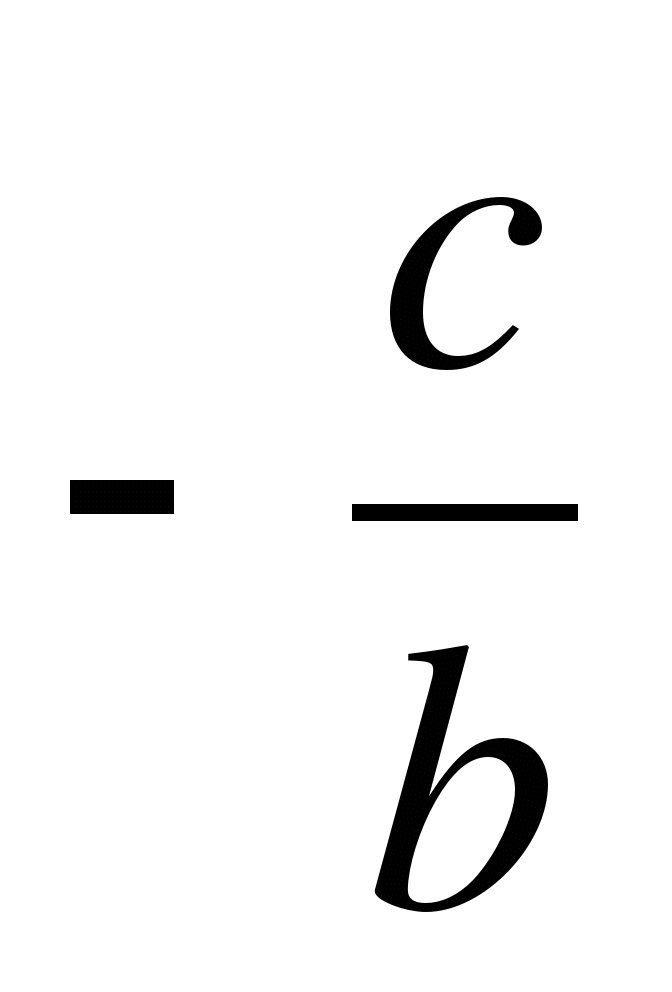
(другой корень найдем, вычитая первый из  ).
).
Из уравнения выводим  .
.
Так как
а
очень малое число, а
х
и
b
не очень велики и не очень малы, то абсолютная величина дроби  очень мала. Пренебрегая этим членом, получим для
х первое приближение
очень мала. Пренебрегая этим членом, получим для
х первое приближение

Вставив это значение в правую часть уравнения (1) , получим второе приближение, более точное чем первое:

Вставив эту величину в первую часть уравнения (1), получим третье приближение , еще более точное. Подобным же путем можем получить, если нужно, четвертое и следующее приближение.
Пример 8.
Решите уравнение: 0,003х 2 + 5х - 2 = 0
Решение:  .
.
Первое приближение = 0,4. Это число более истинного значения х 2 , потому что нам пришлось отбросить отрицательный член – 0,0006х 2 .
Второе приближение = 0,4 – 0,0006·(0,4) 2 = 0,399904. Это число менее истинного значения х 2 число, большее х 2 , отчего вычитаемое увеличилось, а разность уменьшилась.
Третье приближение оказалось бы больше истинного значения х , четвертое меньше и т. д.
Так как 0,4 > х >0,399904, то взяв вместо
х
одно из этих приближений, сделаем ошибку менее 0,4 – 0,399904, т. е. менее 0,0001. Другой корень получится вычитанием найденного корня из  Если для первого корня возьмем число 0,4, то другой – 1667,(6).
Если для первого корня возьмем число 0,4, то другой – 1667,(6).
б) Случай, когда с очень малое число.
Способ последовательного приближения применим и тогда, когда свободный член уравнения очень малое число сравнительно с
а
и
b
. В этом случае один из корней близок к  а другой – весьма малое количество. В этом нетрудно убедиться, если уравнению придать вид
а другой – весьма малое количество. В этом нетрудно убедиться, если уравнению придать вид 
Так как, по предложению, абсолютная величина –
с
очень мала, то уравнение, очевидно, удовлетворится при
х
, или очень близком к 0, или мало отличающемся от 
Чтобы найти корень, имеющий очень малую величину, представим уравнение снова в виде

Так как
а
и
b
суть числа не очень большие и не очень малые, а абсолютная величина
х
2
очень мала, то для первого приближения можно пренебречь членом ; тогда получим
; тогда получим  .
.
Вставив это значение на место х в правую часть уравнения (1), получим второе приближение; подобным же образом найдем, если нужно, и следующие приближения.
4. Решение уравнений с использованием теоремы Виета
(прямой и обратной).
Приведенное квадратное уравнение имеет вид 
Его корни удовлетворяют теореме Виета, которая при
а
=1 имеет вид 
а) Если свободный член q приведенного квадратного уравнения положителен, то уравнение имеет два корня и это зависит от второго коэффициента p . Если p >0 , то оба корня отрицательны, если p <0 , то оба корня положительны.
Пример 9.

 и
и

Пример 10.

 и
и

б) Если свободный член q приведенного уравнения отрицателен, то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p <0, или отрицателен, если p >0 .
Пример 11.

 и
и

Пример 12.

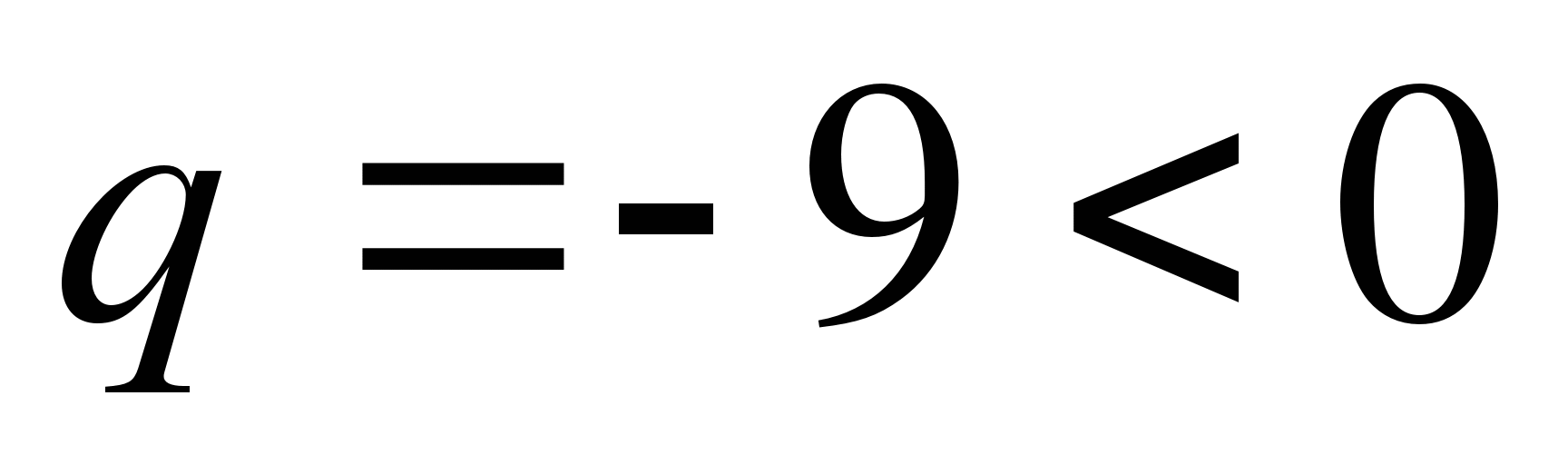 и
и

Пример 13.
Найти корни уравнения: 
Решение: здесь p =-5, q =6. Подберем два числа х 1 и х 2 так, чтобы


По теореме Виета 
Ответ: 
5. Свойства коэффициентов квадратного уравнения.
а) Пусть дано квадратное уравнение 


1. Если а + в + с = 0 (т.е. сумма коэффициентов уравнения равна нулю), то

Доказательство:
Разделим обе части уравнения на
а ≠ 0
, получим приведенное квадратное уравнение 
Согласно теореме Виета 
По условию
а + в + с = 0,
откуда
в = - а – с.
Значит, 
Получаем  что и требовалось доказать.
что и требовалось доказать.
2.
Если
а – в + с = 0, или в = а + с,
то 
Доказательство:
По теореме Виета 
По условию а – в + с = 0 , откуда в = а + с . Таким образом,

т.е.  что и требовалось доказать.
что и требовалось доказать.
3.
Если в уравнении 



Доказательство: Действительно, приведем это уравнение в виде приведенного

Запишем уравнение в виде 
Уравнение, записанное в таком виде, позволяет сразу получить корни

4. Если а = - с = m · n , в = m 2 – n 2 , то корни имеют разные знаки, а именно:

Знаки перед дробями определяются знаком второго коэффициента.
6. Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + b х + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + а b х + ас = 0.
Пусть
ах
= у, откуда
х
=  ; тогда приходим к уравнению
; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильного данному.
Его корни
у
1
и
у
2
найдем с помощью теоремы Виета. Окончательно получаем х
1
=  и х
1
=
и х
1
=  . При этом способе коэффициент
а
умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют
способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент
а
умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют
способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример 14.
Решите уравнение: 2х 2 – 11х + 15 = 0.
Решение: «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение:
у 2 – 11 y + 30 = 0.
Согласно теореме Виета
 Ответ:
2,5; 3.
Ответ:
2,5; 3.
7. Графическое решение квадратного уравнения.
Если в уравнении  перенести второй и третий члены в правую часть, то получим
перенести второй и третий члены в правую часть, то получим 
Построим графики зависимостей  и
и 
График первой зависимости – парабола, проходящая через начало координат. График второй зависимости – прямая (рис.1).

Возможны следующие случаи:
Прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
Прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
Прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет действительных корней. Пример 15.
Решите уравнение: 2 x 2 + 6 x – 5 = 0.
Решение: Разделим уравнение на две части: y = 2 x 2 и y = 6 x – 5.
Построим вспомогательную таблицу:
y = 2 x 2 -57
y = 6 x – 5Построим графики функций y = 2 x 2 и y = 6 x – 5.

Из графика видно, что два уравнения пересекаются в двух точках х 1 и х 2 следовательно уравнение будет иметь два корня х 1 ≈ - 1,1 и х 2 ≈ 2,7.
Ответ: х 1 ≈ - 1,1 и х 2 ≈ 2,7.
8. Решение квадратных уравнений с помощью циркуля и линейки.
Графический способ решения квадратных уравнений с помощью параболы неудобен.
Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаем следующий способ нахождения корней квадратного уравнения
 с помощью циркуля и линейки (рис.5).
с помощью циркуля и линейки (рис.5).
Допустим, что искомая окружность пересекает ось

абсцисс в точках В(х
1
;0) и
D
(х
2
;0), где
х
1
и
х
2
– корни уравнения  и проходит через точки А(0;1) и С
и проходит через точки А(0;1) и С на оси ординат. Тогда по теореме
o
секущих имеем ОВ·О
D
= ОА·ОС, откуда ОС =
на оси ординат. Тогда по теореме
o
секущих имеем ОВ·О
D
= ОА·ОС, откуда ОС = 
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд АС и В D ,поэтому

Итак:
1) построим точки
S (центр окружности) и А(0;1);
(центр окружности) и А(0;1);
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью О х являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1.Радиус окружности больше ординаты центра 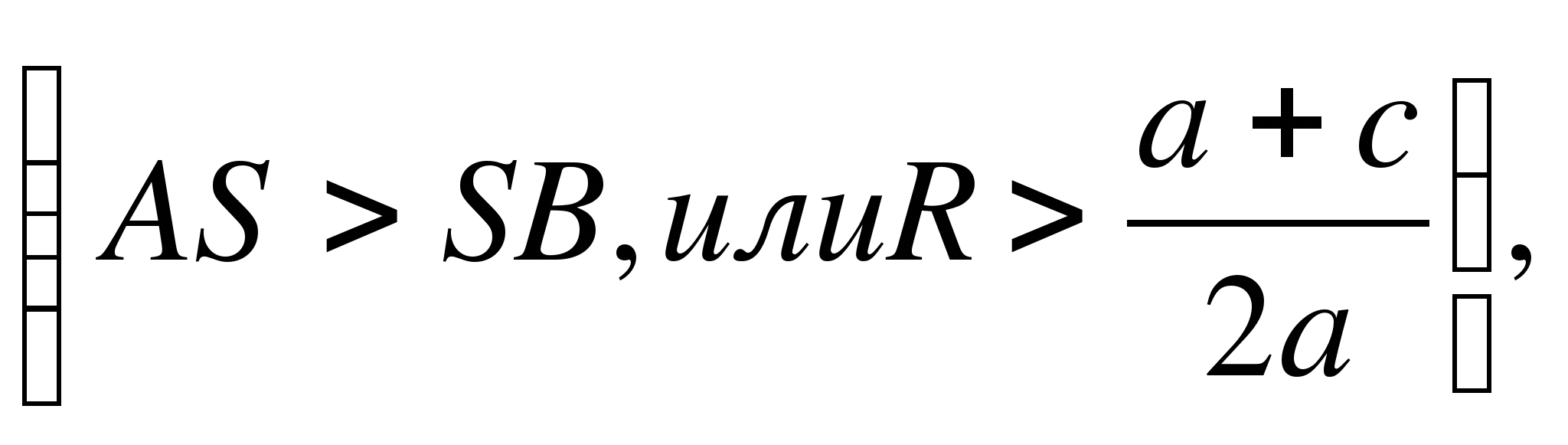 окружность пересекает ось О
х
в двух точках (рис.6,а) В(х
1
;0) и
D
(х
2
;0), где
х
1
и
х
2
окружность пересекает ось О
х
в двух точках (рис.6,а) В(х
1
;0) и
D
(х
2
;0), где
х
1
и
х
2
 1) Радиус окружности больше ординаты центра
1) Радиус окружности больше ординаты центра 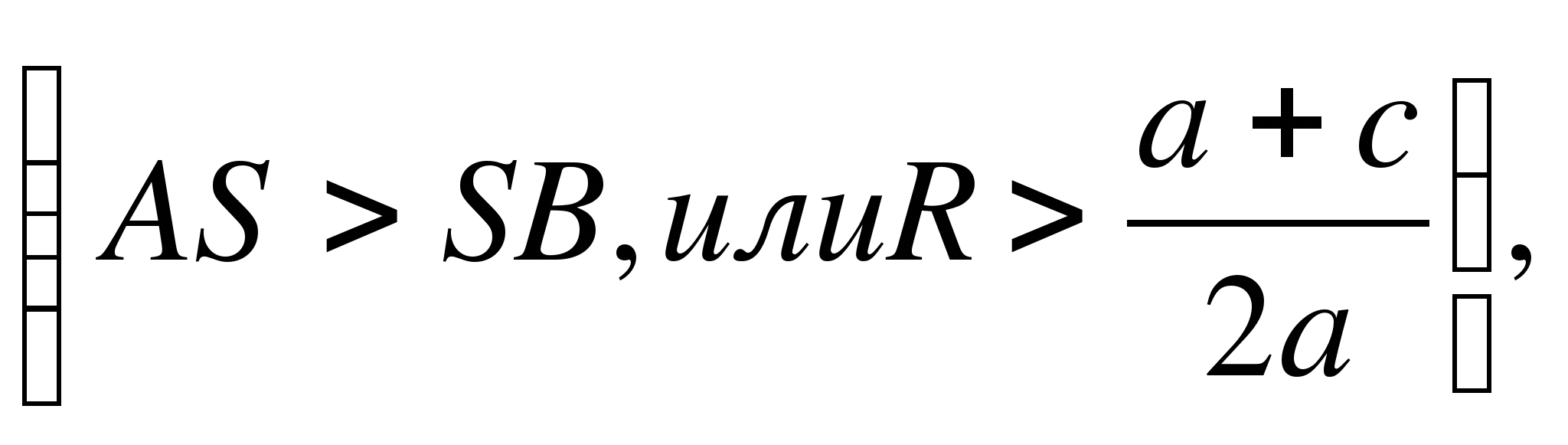 окружность пересекает ось О
х
в двух точках (рис.6,а) В(х
1
;0) и
D
(х
2
;0), где
х
1
и
х
2
– корни квадратного уравнения
окружность пересекает ось О
х
в двух точках (рис.6,а) В(х
1
;0) и
D
(х
2
;0), где
х
1
и
х
2
– корни квадратного уравнения 
2.Радиус окружности равен ординате центра  окружность касается оси О
х
(рис.6,б) в точке В(х
1
;0), где
х
1
– корень квадратного уравнения.
окружность касается оси О
х
(рис.6,б) в точке В(х
1
;0), где
х
1
– корень квадратного уравнения.
3.Радиус окружности меньше ординаты центра  окружность не имеет общих точек с осью абсцисс (рис.6,
в
), в этом случае уравнение не имеет решения.
окружность не имеет общих точек с осью абсцисс (рис.6,
в
), в этом случае уравнение не имеет решения.

а)  Два корня
х
1
и
х
2
.
Два корня
х
1
и
х
2
.
б)  Один корень
х
1
.
Один корень
х
1
.
в)  Нет действительных корней.
Нет действительных корней.
Пример 16.
Решите уравнение: 

Решение: см. рис.7.
Определим координаты центра окружности по формулам:

Проведем окружность радиуса SA , где А (0; 1), S (1; -1).
Ответ: -1; 3.
Пример 17.
Решите уравнение:
 S
см. Брадис В.М
(все в см), из подобия треугольников
S
см. Брадис В.М
(все в см), из подобия треугольников

Пример 20.
Для уравнения
z 2 – 9 z + 8 = 0.
Номограмма дает корни
z 1 = 8, 0 и z 2 = 1, 0 (рис. 12).
Решим с помощью номограммы
номограммы уравнение
2 z 2 – 9 z + 2 = 0.
Разделим коэффициенты этого
уравнения на 2,получим уравнение
z 2 – 4, 5 + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
Пример 21.
Для уравнения

z 2 + 5 z – 6 = 0
номограмма дает положительный
корень z 1 = 1,0, а отрицательный
корень находим, вычитая
положительный корень
из – р, т.е . z 2 = – р – 1 =
= – 5 – 1 = – 6,0 (рис.13.)
10. Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведем ставший знаменитым пример из «Алгебры» ал-Хорезми.
Пример 22.
Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39».
Решение: Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2, 2 = – 8.
у у 3
у 2
3у
3у
9
3
Пример 24.
Решить геометрически уравнения у 2 – 6у – 16 = 0.
Преобразуя уравнение, получаем
у 2 – 6у = 16.
На рис. находим «изображения» выражения у 2 – 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3.
Значит, если к выражению у
2
– 6у прибавить 9, то получим площадь квадрата со стороной у – 3. Заменяя выражение у
2
– 6у равным ему числом, получаем: (у – 3)
2
= 16 +9, т.е. у – 3 = ± или у – 3 = ± 5, где у
1
= 8 и у
2
= – 2.
или у – 3 = ± 5, где у
1
= 8 и у
2
= – 2.
у у 3
у – 3
у – 3
3
3
9
IV. ЗАКЛЮЧЕНИЕ
В результате работы по данной теме можно сделать следующие выводы:
Изучение научно – методической литературы по теме выполненной работы показали, что использование различных способов решения квадратных уравнений является важным звеном при изучении математики, повышает интерес, развивает внимание и сообразительность.
Система использования различных способов решений уравнений на разных этапах урока является эффективным средством активизации обучающихся, положительно влияет на повышение качества знаний, умений и навыков, развивает умственную деятельность.
Основным в решении квадратных уравнений является правильно выбрать рациональный способ решения и применить алгоритм решения.
Работа по данной теме способствует дальнейшему изучению различных способов решений разных уравнений.
V. ЛИТЕРАТУРА
Большая советская энциклопедия. – М., Советская энциклопедия, 1974.
Газета «Математика». – Издательский дом «Первое сентября ».
Глейзер Г.И. История математики в школе. 7-8 классы. – М., Просвещение, 1982.
Детская энциклопедия. Т. 2. – М., Педагогика, 1972.
Дорофеева ВА . Страницы истории на уроках математики. – Львов, Квантор, 1991.
Лиман М.М. Школьникам о математике и математиках. – М., Просвещение, 1981.
Энциклопедия для детей. – М., Аванта +, 1997.
Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классов средней школы. – М., Просвещение, 1981. ;
Брадис В.М. Четырехзначные математические таблицы для средней школы. Изд. 57-е. – М., Просвещение, 1990. С. 83.
Злоцкий Г.В. Карточки-задания при обучении математике. Книга для учителя. – М., Просвещение, 1992.
Клюквин М.Ф. Алгебра, 6-8. Пособие для учащихся 6-8 классов. – М., Просвещение, 1963.
Кужепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. – М., высшая школа, 1969.
Математика (приложение к газете «Первое сентября), №№ 21/96, 10/97, 24/97, 18/98, 21/98.
Окунев А.К . Квадратичные функции, уравнения и неравенства. Пособие для учителя. – М., Просвещение, 1972.
Пресман АА. Решение квадратного уравнения с помощью циркуля и линейки. – М., Квант, № 4/72. С. 34.
Соломник B . C ., Милое П.И. Сборник вопросов и задач по математике. Изд. 4-е, дополн. – М., Высшая школа, 1973.
Худобин А.И . Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. – М., Просвещение,1970.
Лит. Пентковский М. В., Считающие чертежи. (Номограммы), 2 изд., М., 1959;
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ : Разложение левой части уравнения на множители.
Решим уравнение
х 2 + 10х - 24 = 0 .
Разложим левую часть на множители:
х 2 + 10х - 24 = х 2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2 , а также при х = - 12 . Это означает, что число 2 и - 12 являются корнями уравнения х 2 + 10х - 24 = 0 .
2. СПОСОБ: Метод выделения полного квадрата.
Решим уравнение х 2 + 6х - 7 = 0 .
Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2* х * 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2* х * 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
х 2 + 6х - 7 = 0 ,
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х - 7 = х 2 + 2* х * 3 + 3 2 - 3 2 - 7 = (х + 3) 2 - 9 - 7 = (х + 3) 2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 - 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 - 4 = 0, х 1 = 1, или х + 3 = -4, х 2 = -7.
3. СПОСОБ : Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + bх + с = 0, а? 0
на 4а и последовательно имеем:
4а 2 х 2 + 4аbх + 4ас = 0,
((2ах) 2 + 2ах * b + b 2 ) - b 2 + 4ac = 0,
(2ax + b) 2 = b 2 - 4ac,
2ax + b = ± v b 2 - 4ac,
2ax = - b ± v b 2 - 4ac,
Примеры .
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 - 4ac = 7 2 - 4 * 4 * 3 = 49 - 48 = 1,
D > 0, два разных корня;
Таким образом, в случае положительного дискриминанта, т.е. при
b 2 - 4ac >0 , уравнение ах 2 + bх + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1, D = b 2 - 4ac = (-4) 2 - 4 * 4 * 1= 16 - 16 = 0,
D = 0, один корень;
Итак, если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение
ах 2 + bх + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 - 4ac = 3 2 - 4 * 2 * 4 = 9 - 32 = - 13 , D < 0.
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 - 4ac < 0 ,
уравнение ах 2 + bх + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x 1 x 2 = q,
x 1 + x 2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q > 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р < 0 , то оба корня отрицательны, если р < 0 , то оба корня положительны.
Например,
x 2 - 3x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 > 0 и p = - 3 < 0;
x 2 + 8x + 7 = 0; x 1 = - 7 и x 2 = - 1, так как q = 7 > 0 и p= 8 > 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0 ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .
Например,
x 2 + 4x - 5 = 0; x 1 = - 5 и x 2 = 1, так как q= - 5 < 0 и p = 4 > 0;
x 2 - 8x - 9 = 0; x 1 = 9 и x 2 = - 1, так как q = - 9 < 0 и p = - 8 < 0.
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + bх + с = 0, где а? 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + аbх + ас = 0.
Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Окончательно получаем
х 1 = у 1 /а и х 1 = у 2 /а .
При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Решим уравнение 2х 2 - 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 - 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 х 1 = 5/2 x 1 = 2,5
у 2 = 6 x 2 = 6/2 x 2 = 3.
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение
ах 2 + bх + с = 0, где а? 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,
х 2 = с/а.
Доказательство. Разделим обе части уравнения на а? 0, получим приведенное квадратное уравнение
x 2 + b/a * x + c/a = 0.
Согласно теореме Виета
x 1 + x 2 = - b/a,
x 1 x 2 = 1* c/a.
По условию а - b + с = 0, откуда b = а + с. Таким образом,
x 1 + x 2 = - а + b/a= -1 - c/a,
x 1 x 2 = - 1* (- c/a),
т.е. х 1 = -1 и х 2 = c/a , что м требовалось доказать.
1) Решим уравнение 345х 2 - 137х - 208 = 0.
Решение. Так как а + b + с = 0 (345 - 137 - 208 = 0), то
х 1 = 1, х 2 = c/a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х 2 - 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 - 247 + 115 = 0), то
х 1 = 1, х 2 = c/a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2k - четное число, то формулу корней

Пример.
Решим уравнение 3х2 -- 14х + 16 = 0 .
Решение . Имеем: а = 3, b = -- 14, с = 16, k = -- 7 ;
D = k 2 - ac = (- 7) 2 - 3 * 16 = 49 - 48 = 1, D > 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение
х 2 + рх + q= 0
совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней

принимает вид:
Формулу (3) особенно удобно использовать, когда р -- четное число.
Пример. Решим уравнение х 2 - 14х - 15 = 0.
Решение. Имеем: х 1,2 =7±
Ответ: х 1 = 15; х 2 = -1.
7. СПОСОБ: Графическое решение квадратного уравнения.

Если в уравнении
х 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х 2 = - px - q.
Построим графики зависимости у = х 2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости -
прямая (рис.1). Возможны следующие случаи:
Прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квад- ратного уравнения;

Прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
Прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
1) Решим графически уравнение х 2 - 3х - 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4 .
Построим параболу у = х 2 и прямую у = 3х + 4 . Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13) . Прямая и парабола пересекаются в двух точках
А и В с абсциссами х 1 = - 1 и х 2 = 4 . Ответ : х 1 = - 1;
х 2 = 4.

2) Решим графически уравнение (рис. 3) х 2 - 2х + 1 = 0 .
Решение. Запишем уравнение в виде х 2 = 2х - 1 .
Построим параболу у = х 2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N(1/2; 0) . Прямая и парабола пересекаются в точке А с
абсциссой х = 1 . Ответ: х = 1.

3) Решим графически уравнение х 2 - 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х - 5 . Построим параболу у = х 2 и прямую у = 2х - 5 . Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 - 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + bх + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х 1 ; 0) и D (х 2 ; 0), где х 1 и х 2 - корни уравнения ах 2 + bх + с = 0 , и проходит через точки
А(0; 1) и С(0; c/a) на оси ординат. Тогда по теореме о секущих имеем OB * OD = OA * OC , откуда OC = OB * OD / OA= х 1 х 2 / 1 = c/a.
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому

1) построим точки (центр окружности) и A(0; 1) ;
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS > SK, или R > a + c/2a) , окружность пересекает ось Ох в двух точках (рис. 6,а) В(х 1 ; 0) и D(х 2 ; 0) , где х 1 и х 2 - корни квадратного уравнения ах 2 + bх + с = 0 .
2) Радиус окружности равен ординате центра (AS = SB, или R = a + c/2a) , окружность касается оси Ох (рис. 6,б) в точке В(х 1 ; 0) , где х 1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.







Решим уравнение х 2 - 2х - 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:

Проведем окружность радиуса SA, где А (0; 1).
Ответ: х 1 = - 1; х 2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений, помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен там определить корни уравнения.

Криволинейная шкала номограммы построена по формулам (рис.11):
Полагая ОС = р, ED = q, ОЕ = а (все в см.), из подобия треугольников САН и CDF получим пропорцию

откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1) Для уравнения z 2 - 9z + 8 = 0 номограмма дает корни

z 1 = 8,0 и z 2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
2z 2 - 9z + 2 = 0.
Разделим коэффициенты этого уравнения на 2, получим уравнение
z 2 - 4,5z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
3) Для уравнения
z 2 - 25z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5t , получим уравнение
t 2 - 5t + 2,64 = 0,
которое решаем посредством номограммы и получим t 1 = 0,6 и t 2 = 4,4, откуда z 1 = 5t 1 = 3,0 и z 2 = 5t 2 = 22,0.
10. СПОСОБ: Геометрический способ решения квадратных уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.

Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4* 2,5х = 10х) и четырех пристроенных квадратов (6,25* 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим

2) А вот, например, как древние греки решали уравнение у 2 + 6у - 16 = 0 .
Решение представлено на рис. 16, где
у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой один и тот же квадрат, а исходное уравнение у 2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у 1 = 2, у 2 = - 8 (рис.16).

3) Решить геометрически уравнение у 2 - 6у - 16 = 0.
Преобразуя уравнение, получаем
у 2 - 6у = 16.
На рис. 17 находим «изображения» выражения у 2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 - 6у прибавить 9 , то получим площадь квадрата со стороной у - 3 . Заменяя выражение у 2 - 6у равным ему числом 16,
получаем: (у - 3) 2 = 16 + 9, т.е. у - 3 = ± v25 , или у - 3 = ± 5, где у 1 = 8 и у 2 = - 2.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ
Брянская область Жуковский район
МОУ Ржаницкая средняя общеобразовательная школа
ИССЛЕДОВАТЕЛЬСКАЯ РАБОТА
СПОСОБОВ РЕШЕНИЯ
Павликов Дмитрий, 9 кл.
Руководитель: Приходько Юрий
Владимирович,
учитель математики.
БРЯНСК, 2009 год
I . История развития квадратных уравнений ……………………….2
1. Квадратные уравнения в Древнем Вавилоне………………………..2
2. Как составлял и решал Диофант квадратные уравнения…………...2
3. Квадратные уравнения в Индии……………………………………...3
4. Квадратные уравнения у ал- Хорезми ………………………………4
5. Квадратные уравнения в Европе XIII - XVII вв………………..........5
6. О теореме Виета ………………………………………………………6
II . Способы решения квадратных уравнений ……………………….7
Способ…………………………………………………………………7
Способ…………………………………………………………………7
Способ………………………………………………………………....9
Способ………………………………………………………………...10
Способ………………………………………………………………...12
Способ………………………………………………………………...13
Способ………………………………………………………………...15
Способ………………………………………………………………...16
III . Заключение …………………………………………………..............18
Литература ……………………………………………………………….19
История развития квадратных уравнений.
1. Квадратные уравнения в Древнем Вавилоне.
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X 2 + X = ¾; X 2 - X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
2. Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение - 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х , другое же меньше, т.е. 10 - х . Разность между ними 2х .
Отсюда уравнение:
(10 + х)(10 - х) = 96
100 - х 2 = 96
х 2 - 4 = 0 (1)
Отсюда х = 2 . Одно из искомых чисел равно 12 , другое 8 . Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 - у) = 96,
у 2 - 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
3. Квадратные уравнения в Индии.
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах 2 + b х = с, а 0. (1)
В уравнении (1) коэфиценты, кроме а , могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x /8) 2 + 12 = x
Бхаскара пишет под видом:
х 2 - 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
х 2 - 64х + 32 2 = -768 + 1024,
(х - 32) 2 = 256,
х - 32 = ± 16,
х 1 = 16, х 2 = 48.
4. Квадратные уравнения у ал - Хорезми.
В алгебраическом трактате ал - Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах 2 + с = b х.
2) «Квадраты равны числу», т.е. ах 2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах 2 + с = b х.
5) «Квадраты и корни равны числу», т.е. ах 2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах 2 .
Для ал - Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал - джабр и ал - мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида ал - Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал - Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Приведем пример:
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень»
(подразумевается корень уравнения х 2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал - Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
5. Квадратные уравнения в Европе XIII - XVII вв.
Формулы решения квадратных уравнений по образцу ал - Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI - XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
х 2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
6. О теореме Виета.
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D , умноженное на A - A 2 , равно BD , то A равно В и равно D ».
Чтобы понять Виета, следует вспомнить, что А , как и всякая гласная буква, означало у него неизвестное (наше х ), гласные же В, D - коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b )х - х 2 = ab ,
х 2 - (а + b )х + а b = 0,
х 1 = а, х 2 = b .
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
Итак: Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения. Однако имеются и другие способы решения квадратных уравнений, которые позволяют очень быстро и рационально решать многие уравнения. Имеется десять способов решения квадратных уравнений. Подробно в своей работе я разобрала каждый из них.
1. СПОСОБ : Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х - 24 = 0 . Разложим левую часть на множители:
х 2 + 10х - 24 = х 2 + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2 , а также при х = - 12 . Это означает, что число 2 и - 12 являются корнями уравнения х 2 + 10х - 24 = 0 .
2. СПОСОБ : Метод выделения полного квадрата.
Решим уравнение х 2 + 6х - 7 = 0 . Выделим в левой части полный квадрат.
Для этого запишем выражение х 2 + 6х в следующем виде:
х 2 + 6х = х 2 + 2 х 3.
В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2 х 3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
х 2 + 6х - 7 = 0 ,
прибавляя к ней и вычитая 3 2 . Имеем:
х 2 + 6х - 7 = х 2 + 2 х 3 + 3 2 - 3 2 - 7 = (х + 3) 2 - 9 - 7 = (х + 3) 2 - 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 - 16 =0, (х + 3) 2 = 16.
Следовательно, х + 3 - 4 = 0, х 1 = 1, или х + 3 = -4, х 2 = -7.
3. СПОСОБ : Решение квадратных уравнений по формуле.
Умножим обе части уравнения
ах 2 + b х + с = 0, а ≠ 0
на 4а и последовательно имеем:
4а 2 х 2 + 4а b х + 4ас = 0,
((2ах) 2 + 2ах b + b 2 ) - b 2 + 4 ac = 0,
(2ax + b) 2 = b 2 - 4ac,
2ax + b = ± √ b 2 - 4ac,
2ax = - b ± √ b 2 - 4ac,

Примеры .
а) Решим уравнение: 4х 2 + 7х + 3 = 0.
а = 4, b = 7, с = 3, D = b 2 - 4 ac = 7 2 - 4 4 3 = 49 - 48 = 1,
D 0, два разных корня;

Таким образом, в случае положительного дискриминанта, т.е. при
b 2 - 4 ac 0 , уравнение ах 2 + b х + с = 0 имеет два различных корня.
б) Решим уравнение: 4х 2 - 4х + 1 = 0,
а = 4, b = - 4, с = 1, D = b 2 - 4 ac = (-4) 2 - 4 4 1= 16 - 16 = 0,
D = 0, один корень;

 Итак, если дискриминант равен нулю, т.е. b
2
- 4
ac
= 0
, то уравнение
Итак, если дискриминант равен нулю, т.е. b
2
- 4
ac
= 0
, то уравнение
ах 2 + b х + с = 0 имеет единственный корень,
в) Решим уравнение: 2х 2 + 3х + 4 = 0,
а = 2, b = 3, с = 4, D = b 2 - 4 ac = 3 2 - 4 2 4 = 9 - 32 = - 13 , D
Данное уравнение корней не имеет.
Итак, если дискриминант отрицателен, т.е. b 2 - 4 ac , уравнение
ах 2 + b х + с = 0 не имеет корней.
Формула (1) корней квадратного уравнения ах 2 + b х + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет вид
х 2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x 1 x 2 = q ,
x 1 + x 2 = - p
Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).
а) Если сводный член q приведенного уравнения (1) положителен (q 0 ), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p . Если р, то оба корня отрицательны, если р, то оба корня положительны.
Например,
x 2 – 3 x + 2 = 0; x 1 = 2 и x 2 = 1, так как q = 2 0 и p = - 3
x 2 + 8 x + 7 = 0; x 1 = - 7 и x 2 = - 1, так как q = 7 0 и p = 8 0.
б) Если свободный член q приведенного уравнения (1) отрицателен (q ), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p 0 .
Например,
x 2 + 4 x – 5 = 0; x 1 = - 5 и x 2 = 1, так как q = - 5 и p = 4 0;
x 2 – 8 x – 9 = 0; x 1 = 9 и x 2 = - 1, так как q = - 9 и p = - 8
5. СПОСОБ: Решение уравнений способом «переброски».
Рассмотрим квадратное уравнение
ах 2 + b х + с = 0, где а ≠ 0.
Умножая обе его части на а, получаем уравнение
а 2 х 2 + а b х + ас = 0.
Пусть ах = у , откуда х = у/а ; тогда приходим к уравнению
у 2 + by + ас = 0,
равносильно данному. Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Окончательно получаем х 1 = у 1 /а и х 1 = у 2 /а . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски» . Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример.
Решим уравнение 2х 2 – 11х + 15 = 0.
Решение. «Перебросим» коэффициент 2 к свободному члену, в результате получим уравнение
у 2 – 11у + 30 = 0.
Согласно теореме Виета
у 1 = 5 х 1 = 5/2 x 1 = 2,5
у 2 = 6 x 2 = 6/2 x 2 = 3.
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения.
А. Пусть дано квадратное уравнение ах 2 + b х + с = 0, где а ≠ 0.
1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х 1 = 1,
х 2 = с/а.
Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x 2 + b / a x + c / a = 0.
Согласно теореме Виета
x 1 + x 2 = - b / a ,
x 1 x 2 = 1 c / a .
По условию а – b + с = 0, откуда b = а + с. Таким образом,
x 1 + x 2 = - а + b / a = -1 – c / a ,
x 1 x 2 = - 1 (- c / a ),
т.е. х 1 = -1 и х 2 = c / a , что м требовалось доказать.
Примеры.
Решим уравнение 345х 2 – 137х – 208 = 0.
Решение. Так как а + b + с = 0 (345 – 137 – 208 = 0), то
х 1 = 1, х 2 = c / a = -208/345.
Ответ: 1; -208/345.
2)Решим уравнение 132х 2 – 247х + 115 = 0.
Решение. Так как а + b + с = 0 (132 – 247 + 115 = 0), то
х 1 = 1, х 2 = c / a = 115/132.
Ответ: 1; 115/132.
Б. Если второй коэффициент b = 2 k – четное число, то формулу корней

Пример.
Решим уравнение 3х2 - 14х + 16 = 0 .
Решение . Имеем: а = 3, b = - 14, с = 16, k = - 7 ;
D = k 2 – ac = (- 7) 2 – 3 16 = 49 – 48 = 1, D 0, два различных корня;
Ответ: 2; 8/3
В. Приведенное уравнение
х 2 + рх + q = 0
совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней

принимает вид:
Формулу (3) особенно удобно использовать, когда р - четное число.
Пример. Решим уравнение х 2 – 14х – 15 = 0.
Решение. Имеем: х 1,2 =7±
Ответ: х 1 = 15; х 2 = -1.
7. СПОСОБ: Графическое решение квадратного уравнения.
Е сли в уравнении
сли в уравнении
х 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
х 2 = - px - q .
Построим графики зависимости у = х 2 и у = - px - q.
График первой зависимости - парабола, проходящая через начало координат. График второй зависимости -
прямая (рис.1). Возможны следующие случаи:
Прямая и парабола могут пересекаться в двух точках,
 абсциссы точек пересечения являются корнями квад- ратного уравнения;
абсциссы точек пересечения являются корнями квад- ратного уравнения;
Прямая и парабола могут касаться (только одна общая точка), т.е. уравнение имеет одно решение;
Прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Примеры.
1) Решим графически уравнение х 2 - 3х - 4 = 0 (рис. 2).
Решение. Запишем уравнение в виде х 2 = 3х + 4 .
Построим параболу у = х 2 и прямую у = 3х + 4 . Прямую
у = 3х + 4 можно построить по двум точкам М (0; 4) и
N (3; 13) . Прямая и парабола пересекаются в двух точках
А и В с абсциссами х 1 = - 1 и х 2 = 4 . Ответ : х 1 = - 1;
х 2 = 4.

2) Решим графически уравнение (рис. 3) х 2 - 2х + 1 = 0 .
Решение. Запишем уравнение в виде х 2 = 2х - 1 .
Построим параболу у = х 2 и прямую у = 2х - 1.
Прямую у = 2х - 1 построим по двум точкам М (0; - 1)
и N (1/2; 0) . Прямая и парабола пересекаются в точке А с
абсциссой х = 1 . Ответ: х = 1.

3) Решим графически уравнение х 2 - 2х + 5 = 0 (рис. 4).
Решение. Запишем уравнение в виде х 2 = 5х - 5 . Построим параболу у = х 2 и прямую у = 2х - 5 . Прямую у = 2х - 5 построим по двум точкам М(0; - 5) и N(2,5; 0). Прямая и парабола не имеют точек пересечения, т.е. данное уравнение корней не имеет.
Ответ. Уравнение х 2 - 2х + 5 = 0 корней не имеет.
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и
линейки.

Графический способ решения квадратных уравнений с помощью параболы неудобен. Если строить параболу по точкам, то требуется много времени, и при этом степень точности получаемых результатов невелика.
Предлагаю следующий способ нахождения корней квадратного уравнения ах 2 + b х + с = 0 с помощью циркуля и линейки (рис. 5).
Допустим, что искомая окружность пересекает ось
абсцисс в точках В(х 1 ; 0) и D (х 2 ; 0), где х 1 и х 2 - корни уравнения ах 2 + b х + с = 0 , и проходит через точки
А(0; 1) и С(0; c / a ) на оси ординат. Тогда по теореме о секущих имеем OB OD = OA OC , откуда OC = OB OD / OA = х 1 х 2 / 1 = c / a .
Центр окружности находится в точке пересечения перпендикуляров SF и SK , восстановленных в серединах хорд AC и BD , поэтому

1) построим точки (центр окружности) и A (0; 1) ;
2) проведем окружность с радиусом SA ;
3) абсциссы точек пересечения этой окружности с осью Ох являются корнями исходного квадратного уравнения.
При этом возможны три случая.
1) Радиус окружности больше ординаты центра (AS SK , или R a + c /2 a ) , окружность пересекает ось Ох в двух точках (рис. 6,а) В(х 1 ; 0) и D (х 2 ; 0) , где х 1 и х 2 - корни квадратного уравнения ах 2 + b х + с = 0 .
2) Радиус окружности равен ординате центра (AS = SB , или R = a + c /2 a ) , окружность касается оси Ох (рис. 6,б) в точке В(х 1 ; 0) , где х 1 - корень квадратного уравнения.
3) Радиус окружности меньше ординаты центра
окружность не имеет общих точек с осью абсцисс (рис.6,в), в этом случае уравнение не имеет решения.
Пример.
Решим уравнение х 2 - 2х - 3 = 0 (рис. 7).
Решение. Определим координаты точки центра окружности по формулам:
Проведем окружность радиуса SA, где А (0; 1).
Ответ: х 1 = - 1; х 2 = 3.
9. СПОСОБ: Решение квадратных уравнений с помощью
номограммы.
Это старый и незаслуженно забыты способ решения квадратных уравнений,
помещенный на с.83 (см. Брадис В.М. Четырехзначные математические таблицы. - М., Просвещение, 1990).
Таблица XXII. Номограмма для решения уравнения z 2 + pz + q = 0 . Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициен-
там определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.11):
Полагая ОС = р, ED = q , ОЕ = а (все в см.), из
подобия треугольников САН и CDF получим
пропорцию
откуда после подстановок и упрощений вытекает уравнение
z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
Примеры.
1) Для уравнения z 2 - 9 z + 8 = 0 номограмма дает корни z 1 = 8,0 и z 2 = 1,0 (рис.12).
2) Решим с помощью номограммы уравнение
2 z 2 - 9 z + 2 = 0.
Разделим коэффициенты этого уравнения на 2,
получим уравнение
z 2 - 4,5 z + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
3) Для уравнения
z 2 - 25 z + 66 = 0
коэффициенты p и q выходят за пределы шкалы, выполним подстановку z = 5 t ,
получим уравнение
t 2 - 5 t + 2,64 = 0,
которое решаем посредством номограммы и получим t 1 = 0,6 и t 2 = 4,4, откуда z 1 = 5 t 1 = 3,0 и z 2 = 5 t 2 = 22,0.
10. СПОСОБ: Геометрический способ решения квадратных
уравнений.
В древности, когда геометрия была более развита, чем алгебра, квадратные уравнения решали не алгебраически, а геометрически. Приведу ставший знаменитым пример из «Алгебры» ал - Хорезми.
Примеры.
1) Решим уравнение х 2 + 10х = 39.
В оригинале эта задача формулируется следующим образом: «Квадрат и десять корней равны 39» (рис.15).
Решение. Рассмотрим квадрат со стороной х, на его сторонах строятся прямоугольники так, что другая сторона каждого из них равна 2,5, следовательно, площадь каждого равна 2,5х. Полученную фигуру дополняют затем до нового квадрата ABCD, достраивая в углах четыре равных квадрата, сторона каждого их них 2,5, а площадь 6,25.
Площадь S квадрата ABCD можно представить как сумму площадей: первоначального квадрата х 2 , четырех прямоугольников (4 2,5х = 10х) и четырех пристроенных квадратов (6,25 4 = 25) , т.е. S = х 2 + 10х + 25. Заменяя
х 2 + 10х числом 39 , получим, что S = 39 + 25 = 64 , откуда следует, что сторона квадрата ABCD , т.е. отрезок АВ = 8 . Для искомой стороны х первоначального квадрата получим
2) А вот, например, как древние греки решали уравнение у 2 + 6у - 16 = 0 .
Решение представлено на рис. 16, где
у 2 + 6у = 16, или у 2 + 6у + 9 = 16 + 9.
Решение. Выражения у 2 + 6у + 9 и 16 + 9 геометрически представляют собой
один и тот же квадрат, а исходное уравнение у 2 + 6у - 16 + 9 - 9 = 0 - одно и то же уравнение. Откуда и получаем, что у + 3 = ± 5, или у 1 = 2, у 2 = - 8 (рис.16).
3) Решить геометрически уравнение у 2 - 6у - 16 = 0.
Преобразуя уравнение, получаем
у 2 - 6у = 16.
На рис. 17 находим «изображения» выражения у 2 - 6у, т.е. из площади квадрата со стороной у два раза вычитается площадь квадрата со стороной, равной 3 . Значит, если к выражению у 2 - 6у прибавить 9 , то получим площадь квадрата со стороной у - 3 . Заменяя выражение у 2 - 6у равным ему числом 16,
получаем: (у - 3) 2 = 16 + 9, т.е. у - 3 = ± √25 , или у - 3 = ± 5, где у 1 = 8 и у 2 = - 2.
Заключение
Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.
Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.
Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.
Здесь мы остановилась на вопросе решения квадратных уравнений, а что, если существуют и другие способы их решения?! Опять находить красивые закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое. Но это вопросы уже следующих работ.
Подводя итоги, можно сделать вывод: квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза. Эти знания могут пригодиться нам на протяжении всей жизни.
Так как эти методы решения квадратных уравнений просты в применении, то они, безусловно, должно заинтересовать увлекающихся математикой учеников. Наша работа дает возможность по-другому посмотреть на те задачи, которые ставит перед нами математика.
Литература:
1. Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. - М., Просвещение, 1981.
2. Брадис В.М. Четырехзначные математические таблицы для средней школы.
Изд. 57-е. - М., Просвещение, 1990. С. 83.
3. Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969.
4. Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1972.
5. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/72. С. 34.
6. Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. - 4-е, дополн. - М., Высшая школа, 1973.
7. Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. - М., Просвещение, 1970.
Заявка на руководство
исследовательской работой
Руководитель: Приходько Юрий Владимирович (учитель математики)
Предполагаемая тема: «10 способов решения квадратных уравнений »
Консультанты:
Приходько Юрий Владимирович (учитель математики);
Ерошенков Дмитрий Александрович (учитель информатики)
Образовательная область знания, учебный предмет, в рамках которого проводится работа по проекту математика
Учебные дисциплины, близкие к теме проекта: математика
Класс обучения: 9 класс
Состав исследовательской группы: Курсин Дмитрий, Павликов Дмитрий
Вид проекта по доминирующей деятельности учащегося: исследование рациональных способов решения квадратных уравнений
Вид проекта по продолжительности: долгосрочный
Вид образования: элективный курс
Необходимое оборудование: научно-популярная литература, связанная с рассмотрением различных способов решения квадратных уравнений
Предполагаемый продукт проекта: создание учебно-методического материала по применению рациональных способов решения квадратных уравнений
Копьевская сельская средняя общеобразовательная школа
10 способов решения квадратных уравнений
Руководитель: Патрикеева Галина Анатольевна,
учитель математики
с.Копьево, 2007
1. История развития квадратных уравнений
1.1 Квадратные уравнения в Древнем Вавилоне
1.2 Как составлял и решал Диофант квадратные уравнения
1.3 Квадратные уравнения в Индии
1.4 Квадратные уравнения у ал- Хорезми
1.5 Квадратные уравнения в Европе XIII - XVII вв
1.6 О теореме Виета
2. Способы решения квадратных уравнений
Заключение
Литература
1. История развития квадратных уравнений
1.1 Квадратные уравнения в Древнем Вавилоне
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения умели решать около 2000 лет до н. э. вавилоняне.
Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются, кроме неполных, и такие, например, полные квадратные уравнения:
X 2 + X = ¾; X 2 - X = 14,5
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современным, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решениями, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствуют понятие отрицательного числа и общие методы решения квадратных уравнений.
1.2 Как составлял и решал Диофант квадратные уравнения.
В «Арифметике» Диофанта нет систематического изложения алгебры, однако в ней содержится систематизированный ряд задач, сопровождаемых объяснениями и решаемых при помощи составления уравнений разных степеней.
При составлении уравнений Диофант для упрощения решения умело выбирает неизвестные.
Вот, к примеру, одна из его задач.
Задача 11. «Найти два числа, зная, что их сумма равна 20, а произведение - 96»
Диофант рассуждает следующим образом: из условия задачи вытекает, что искомые числа не равны, так как если бы они были равны, то их произведение равнялось бы не 96, а 100. Таким образом, одно из них будет больше половины их суммы, т.е. 10 + х , другое же меньше, т.е. 10 - х . Разность между ними 2х .
Отсюда уравнение:
(10 + х)(10 - х) = 96
100 - х 2 = 96
х 2 - 4 = 0 (1)
Отсюда х = 2 . Одно из искомых чисел равно 12 , другое 8 . Решение х = -2 для Диофанта не существует, так как греческая математика знала только положительные числа.
Если мы решим эту задачу, выбирая в качестве неизвестного одно из искомых чисел, то мы придем к решению уравнения
у(20 - у) = 96,
у 2 - 20у + 96 = 0. (2)
Ясно, что, выбирая в качестве неизвестного полуразность искомых чисел, Диофант упрощает решение; ему удается свести задачу к решению неполного квадратного уравнения (1).
1.3 Квадратные уравнения в Индии
Задачи на квадратные уравнения встречаются уже в астрономическом тракте «Ариабхаттиам», составленном в 499 г. индийским математиком и астрономом Ариабхаттой. Другой индийский ученный, Брахмагупта (VII в.), изложил общее правило решения квадратных уравнений, приведенных к единой канонической форме:
ах 2 + b х = с, а > 0. (1)
В уравнении (1) коэфиценты, кроме а , могут быть и отрицательными. Правило Брахмагупты по существу совпадает с нашим.
В Древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму.
Вот одна из задач знаменитого индийского математика XII в. Бхаскары.
Задача 13.
«Обезьянок резвых стая А двенадцать по лианам…
Власть поевши, развлекалась. Стали прыгать, повисая…
Их в квадрате часть восьмая Сколько ж было обезьянок,
На поляне забавлялась. Ты скажи мне, в этой стае?»
Решение Бхаскары свидетельствует о том, что он знал о двузначности корней квадратных уравнений (рис. 3).
Соответствующее задаче 13 уравнение:
(x /8) 2 + 12 = x
Бхаскара пишет под видом:
х 2 - 64х = -768
и, чтобы дополнить левую часть этого уравнения до квадрата, прибавляет к обеим частям 32 2 , получая затем:
х 2 - 64х + 32 2 = -768 + 1024,
(х - 32) 2 = 256,
х - 32 = ± 16,
х 1 = 16, х 2 = 48.
1.4 Квадратные уравнения у ал – Хорезми
В алгебраическом трактате ал - Хорезми дается классификация линейных и квадратных уравнений. Автор насчитывает 6 видов уравнений, выражая их следующим образом:
1) «Квадраты равны корнями», т.е. ах 2 + с = b х.
2) «Квадраты равны числу», т.е. ах 2 = с.
3) «Корни равны числу», т.е. ах = с.
4) «Квадраты и числа равны корням», т.е. ах 2 + с = b х.
5) «Квадраты и корни равны числу», т.е. ах 2 + bx = с.
6) «Корни и числа равны квадратам», т.е. bx + с = ах 2 .
Для ал - Хорезми, избегавшего употребления отрицательных чисел, члены каждого их этих уравнений слагаемые, а не вычитаемые. При этом заведомо не берутся во внимание уравнения, у которых нет положительных решений. Автор излагает способы решения указанных уравнений, пользуясь приемами ал - джабр и ал - мукабала. Его решения, конечно, не совпадает полностью с нашим. Уже не говоря о том, что оно чисто риторическое, следует отметить, например, что при решении неполного квадратного уравнения первого вида
ал - Хорезми, как и все математики до XVII в., е учитывает нулевого решения, вероятно, потому, что в конкретных практических задачах оно не имеет значения. При решении полных квадратных уравнений ал - Хорезми на частных числовых примерах излагает правила решения, а затем и геометрические доказательства.
Задача 14. «Квадрат и число 21 равны 10 корням. Найти корень» (подразумевается корень уравнения х 2 + 21 = 10х).
Решение автора гласит примерно так: раздели пополам число корней, получишь 5, умножишь 5 само на себя, от произведения отними 21, останется 4. Извлеки корень из 4, получишь 2. Отними 2 от5, получишь 3, это и будет искомый корень. Или же прибавь 2 к 5, что даст 7, это тоже есть корень.
Трактат ал - Хорезми является первой, дошедшей до нас книгой, в которой систематически изложена классификация квадратных уравнений и даны формулы их решения.
1.5 Квадратные уравнения в Европе XIII - XVII вв
Формулы решения квадратных уравнений по образцу ал - Хорезми в Европе были впервые изложены в « Книге абака», написанной в 1202 г. итальянским математиком Леонардо Фибоначчи. Этот объемистый труд, в котором отражено влияние математики, как стран ислама, так и Древней Греции, отличается и полнотой, и ясностью изложения. Автор разработал самостоятельно некоторые новые алгебраические примеры решения задач и первый в Европе подошел к введению отрицательных чисел. Его книга способствовала распространению алгебраических знаний не только в Италии, но и в Германии, Франции и других странах Европы. Многие задачи из « Книги абака» переходили почти во все европейские учебники XVI - XVII вв. и частично XVIII.
Общее правило решения квадратных уравнений, приведенных к единому каноническому виду:
х 2 + bx = с,
при всевозможных комбинациях знаков коэффициентов b , с было сформулировано в Европе лишь в 1544 г. М. Штифелем.
Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. Учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. Благодаря труда Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
1.6 О теореме Виета
Теорема, выражающая связь между коэффициентами квадратного уравнения и его корнями, носящая имя Виета, была им сформулирована впервые в 1591 г. следующим образом: «Если B + D , умноженное на A - A 2 , равно BD , то A равно В и равноD ».
Чтобы понять Виета, следует вспомнить, что А , как и всякая гласная буква, означало у него неизвестное (наше х ), гласные же В, D - коэффициенты при неизвестном. На языке современной алгебры вышеприведенная формулировка Виета означает: если имеет место
(а + b )х - х 2 = ab ,
х 2 - (а + b )х + а b = 0,
х 1 = а, х 2 = b .
Выражая зависимость между корнями и коэффициентами уравнений общими формулами, записанными с помощью символов, Виет установил единообразие в приемах решения уравнений. Однако символика Виета еще далека от современного вида. Он не признавал отрицательных чисел и по этому при решении уравнений рассматривал лишь случаи, когда все корни положительны.
2. Способы решения квадратных уравнений
Квадратные уравнения - это фундамент, на котором покоится величественное здание алгебры. Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания вуза.
ПроектТворческое название проекта
ДЕВИЗ: В математике большую роль играют маленькие хитрости.
Автор проекта: Рылова Виктория
ученица 8Г класса МОУ СОШ №1
с углубленным изучением
отдельных предметов «Полифорум»Основополагающий вопрос проекта:
«Насколько разнообразны способы решения
квадратных уравнений?»
Гипотеза:
Предполагаю, что квадратные уравнения можно решить
несколькими разными способами
Цель:
Изучение теоретических основ и применение на
практике различных способов решения квадратных
уравненийЗадачи:
1. Подобрать информацию по теме из письменных
источников и сети Интернет
2. Синтезировать информацию по плану
3. Изучить различные способы решения квадратных
уравнений и апробировать материал на практике
План работы:
Определение темы и цели проекта,
формулирование темы исследования
Определение источника информации
Определение способа сбора и анализа
информации
Определение способа представления
результатов
Аннотация
Проект "Способы решения квадратныхуравнений" отражает результаты исследования,
проведенного мной о том, какие существуют
способы решения квадратных уравнений и что из
этого можно взять полезного для себя и моих
друзей.
Тема проекта связана с тем, чтобы, используя
способы решения квадратных уравнений можно
найти неизвестное об известном.
В школьном курсе математики изучаются
формулы корней квадратных уравнений, с
помощью которых можно решать любые
квадратные уравнения.
Однако имеются и другие приёмы решения
уравнений, которые позволяют очень быстро и
рационально решать квадратные уравнения.Из истории квадратных
уравнений
Квадратные уравнения умели решать около 2000 лет
до н. э. вавилоняне. Применяя современную
алгебраическую запись, можно сказать, что в их
клинописных текстах встречаются, кроме неполных, и
такие, например, полные квадратные уравнения:
Почти все найденные до сих пор клинописные
тексты приводят только задачи с решениями,
изложенными в виде рецептов, без указаний
относительно того, каким образом они были
найдены.Индийский ученый Брахмагупта (VII в.),
изложил общее правило решения
квадратных уравнений, приведенных к
единой канонической форме:
ах2 + bх = с, а > 0
В уравнении коэффициенты, кроме а,
могут быть отрицательными. Правило
Брахмагупта по существу совпадает с
нашим.
Брахмагупта
Формулы решения квадратных уравнений
были впервые изложены в книге,
написанной итальянским математиком
Леонардо Фибоначчи (XIIIв.). х2 + bх = с,
при всевозможных комбинациях знаков
коэффициентов b, с было
сформулировано в Европе лишь в 1544 г.
Леонардо ФибоначчиЛишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и
других ученых способ решения квадратных уравнений
принимает современный вид.
Я мыслю,
следовательно,
существую.
Декарт
Гений есть
терпение мысли,
сосредоточенной
в известном
направлении.
Ньютон
Все уравнения
алгебры имеют
столько решений,
сколько их
показывает
наименование
наивысшей
величины.
Жирар
Все математики
знали, что под
алгеброй были скрыты
несравненные
сокровища, но не
умели их найти
ВиетГеометрический
способ решения
квадратных
уравнений
Решение
квадратных
уравнений
с помощью
номограммы
Решение
квадратных
уравнений
с помощью циркуля
и линейки
Решения
квадратных
уравнений
способом
«переброски»
Разложение
левой
части уравнения
на множители
Различные
способы
решения
квадратных
уравнений
Графическое
решение
квадратного
уравнения
Метод
выделения
полного квадрата
Метод
коэффициентов
Решение
квадратных
уравнений
по формуле
Решение
уравнений
с использованием
теоремы Виета
1. СПОСОБ: Разложение левой части уравнения на множители
Цель:привести квадратное уравнение
общего вида к виду
А(х)·В(х)=0,
где А(х) и В(х) –
многочлены относительно х.
Способы:
Вынесение общего множителя за
скобки;
Использование формул
сокращенного умножения;
Способ группировки.
Решим уравнение
х2 + 10х - 24 = 0.
Разложим левую часть на множители:
х2 + 10х - 24 =
=(х + 12)(х - 2).
Следовательно,
(х + 12)(х - 2) = 0
Так как произведение равно нулю, то,
один из его множителей равен нулю. Поэтому левая часть
уравнения обращается нуль при х = 2, а также при х = - 12.
Это означает, что число 2 и - 12 являются корнями
уравнения х2 + 10х - 24 = 0.
2. СПОСОБ: Метод выделения полного квадрата.
Суть метода: привести квадратное уравнение общего вида кнеполному квадратному уравнению.
Решим уравнение х2 + 6х - 7 = 0.
Выделим в левой части полный квадрат.
Преобразуем теперь левую часть уравнения
х2 + 6х - 7 = 0, прибавляя к ней и вычитая 9.
Имеем:
х2 + 6х - 7 =
=х2 + 2 х 3 + 9 - 9 - 7 =
= (х + 3)2 - 9 - 7 = (х + 3)2 - 16.
Таким образом, данное уравнение можно записать
так:
(х + 3)2 - 16 =0,
(х + 3)2 = 16.
Следовательно, х + 3 - 4 = 0, или х + 3 = -4
х1 = 1,
х2 = -7.3. СПОСОБ: Решение квадратных
уравнений по формуле
a 1
b 0, c 0
D >0
2корня
D =0
1корень
x px g 0
2
D<0 Нет корней
Формулы корней:
2
1
x1,2
p
2
b b 2 4ac
x1, 2
;
2a
2
p
g;
4
3
x1, 2
k k 2 ac
a
4. СПОСОБ: Решение уравнений с использованием теоремы Виета.
Как известно, приведенное квадратное уравнение имеет видх2 + px + c = 0. (1)
Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид
x1 x2 = q,
Отсюда можно сделать следующие выводы
x1 + x2 = - p
(по коэффициентам p и q можно предсказать знаки
корней).
Если (q > 0), то уравнение имеет два одинаковых по
знаку корня и это зависти от второго коэффициента p.
Если р < 0, то оба корня отрицательны.
Если р < 0, то оба корня положительны.
5. СПОСОБ: Решение уравнений способом «переброски».
При этом способе коэффициент а умножается на свободный член, как бы«перебрасывается» к нему, поэтому его называют способом «переброски».
Этот способ применяют, когда можно легко найти корни уравнения,
используя теорему Виета и, что самое важное, когда дискриминант есть
точный квадрат
Решим уравнение 2х2 – 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену, в
результате получим уравнение
у2 – 11у + 30 = 0.
Согласно теореме Виета у = 5, у =6, то х1 = 5/2, х = 6/2
Ответ: 2,5; 3.
6. СПОСОБ: Свойства коэффициентов квадратного уравнения
Пусть дано квадратное уравнениеах2 + bх + с = 0, где а ≠ 0.
Если, а+ b + с = 0 , то
x1 1, x2
c
a
Если b = a + c, то
x1 1, x2
c
a
1978 x 1984 x 6 0
2
x1 1;
6
x2
1978
319 x 2 1988 x 1669 0
x1 1;
1669
x2
.
319
7. СПОСОБ: Графическое решение квадратного уравнения
преобразуем уравнениех2 + px + q = 0
х2 = - px - q.
Построим графики зависимости у = х2 и у = - px - q.
График первой зависимости - парабола, проходящая
через начало координат. График второй
зависимости - прямая (рис.1). Возможны следующие
случаи:
Прямая и
парабола могут
касаться (только
одна общая
точка), т.е.
уравнение имеет
одно решение;
прямая и
парабола не
имеют общих точек,
т.е. квадратное
уравнение не имеет
корней.
прямая и парабола
могут пересекаться в
двух точках, абсциссы
точек
пересечения
являются
корнями
квадратного
уравнения;
8. СПОСОБ: Решение квадратных уравнений с помощью циркуля и линейки.
ах2 + bх + с =0Итак:
1) построим точки (центр окружности)
и A(0; 1);
2) проведем окружность с радиусом
SA;
3) абсциссы точек пересечения этой
окружности с осью Ох являются
корнями исходного квадратного
уравнения.
2)окружность касается оси Ох в
При этом возможны три случая.
1)окружность пересекает ось
Ох в двух точках
В(х1;0) и D(х2; 0), где х1 и х2
- корни квадратного
уравнения ах² + bх + с = 0.
точке В(х1; 0), где х1 - корень
квадратного уравнения.
3) окружность не имеет общих
точек с осью абсцисс (рис.6,в), в
этом случае уравнение не имеет
решения.
9. СПОСОБ: Решение квадратных уравнений с помощью номограммы.
Таблица XXII. с.83 (см. Брадис В.М. Четырехзначныематематические таблицы. - М., Просвещение,
1990).
Номограмма для решения уравнения
z2 + pz + q = 0. Эта номограмма позволяет,
не решая квадратного уравнения,
по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена
по формулам (рис.11):
z2 + pz + q = 0,
причем буква z означает метку любой
точки криволинейной шкалы.10. СПОСОБ: Геометрический способ
решения квадратных уравнений.
Как древние греки решали
уравнение у2 + 6y – 16 = 0.
Решение представлено на
рисунке, где у2 + 6у = 16,
или у2 + 6 у + 9 = 16 + 9.
Выражения у2 + 6у + 9 и 16 + 9
геометрически представляют
собой один и тот же квадрат, а
исходное уравнение у2 + 6у – 16
+ 9 – 9 = 0 – одно и то же
уравнение. Откуда и получаем,
что у + 3 = + 5 и у + 3 = – 5, или
у =2, у2= –8
у
3
у
у2
3
3у
3у
9 моя работа дает возможность по-другому
посмотреть на те задачи, которые ставит
перед нами математика.
данные приёмы решения заслуживают
внимания,
поскольку они не отражены в
школьных учебниках математики;
овладение данными приёмами помогает мне
экономить время и эффективно решать
уравнения;
потребность в быстром решении
обусловлена применением тестовой системы
выпускных экзаменов;
Заключение
«В математике следует помнить неформулы, а процессы мышления»
В.П.Ермаков
